9 The value of lim n → ∞ ( 1 n 1 1 n 2 1 6 n) is WBJEE 08 10 Here, x denotes the greatest integer less than or equal to x Given that f ( x) = x x The value obtained when this function is integrated with respect to x with lower limit as $$\lim_{n \rightarrow \infty} \dfrac{(sin(\dfrac{1}{n}))^2}{n^2})$$ Steps I have taken Getting rid of the square through the limit of a product is the product of it's limit so I will square the limit at the endThus ∑ n n 2 1 diverges by the Limit Comparison Test • If x =1 the series becomes ∞ ∑ n =1 (1) n1 n n 2 1 which converges by the Alternating Series Test since {n n 2 1} is a positive decreasing sequence with lim n →∞ n n 2 1 = 0 Thus, IOC = 1, 1) Observe While f (x) and f 0 (x) had the same radii of convergence

Limit Replace 1 By 0 Mathematics Stack Exchange
Lim (1 1/n^2)(1 2/n^2)...(1 n/n^2)
Lim (1 1/n^2)(1 2/n^2)...(1 n/n^2)-Lim 3−2n4n2 4n25n−3 lim 3 − 2 n 4 n 2 4 n 2 5 n − 3 có giá trị là bao nhiêu?Nếu limun = L lim u n = L thì lim 1 3√un8 lim 1 u n 8 3 có giá trị là bao
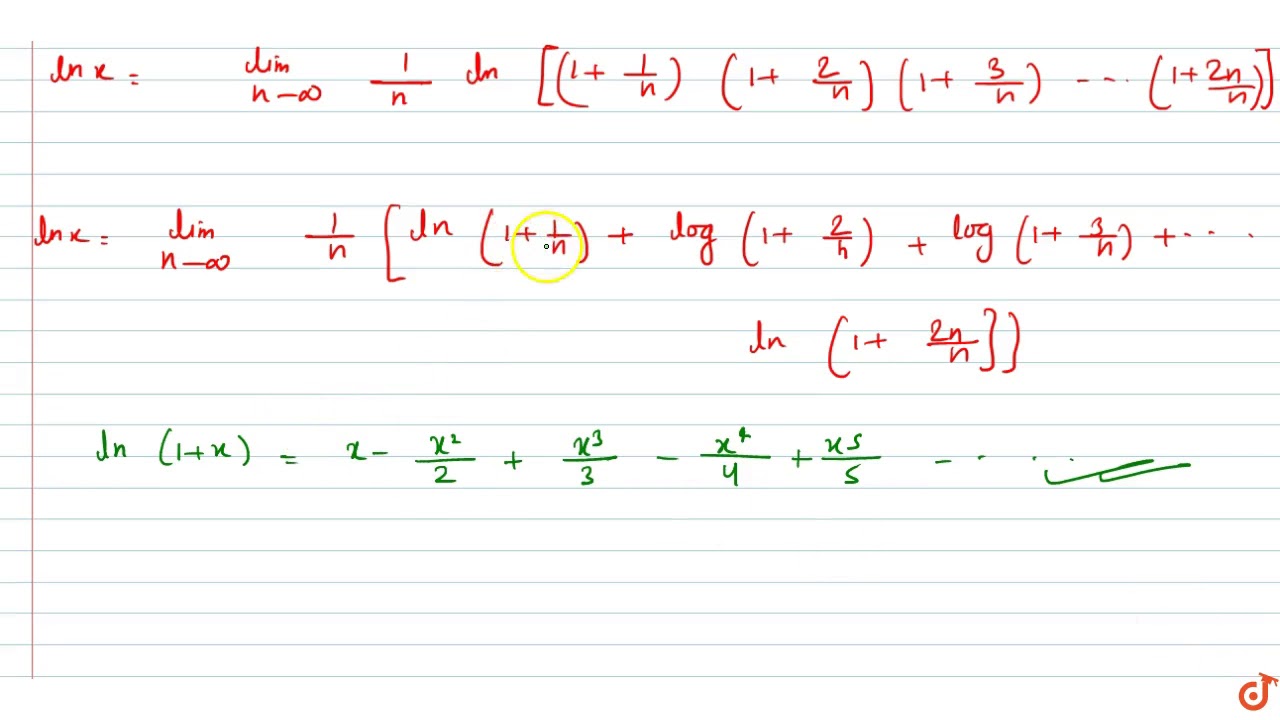



Lim N Gtoo N 1 N 2 3n N 2n 1 N Is Equal To Youtube
So in this case, the limit has to be zero, because the denominator approaches infinity WAY faster *I also just noticed that factoring out the 2 n will also take out every single term in the numerator 2n4 = 2 (n2), so goodbye n2 term;Lim N → ∞ 1 2 2 2 3 2 N 2 N 3 CBSE CBSE (Commerce) Class 11 Textbook Solutions 79 Important Solutions 14 Question Bank Solutions 6793 Concept Notes & Videos 3 Syllabus Advertisement Remove all ads Lim N → ∞ 1 2 2 2 3 2 N 2 N 3Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
Nếu limun = L lim u n = L thì lim√un 9 lim u n 9 có giá trị là bao nhiêu?\left( n 1 \right)!}{\left( n 2 \right)!If a_n = (1)^n(n^2)/(2n^2 2n 1), then lim a_n = (A) 1/2 (B) 1/2 0 (D) does not exist (E) None of these Previous question Next question Get more help from Chegg
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreHomework Equations The Attempt at a Solution I believe it does converge because the higher power is in the denominator, so thus, it's limit is 0 Any help or hints on if I'm headed in the right direction would be very much appreciated!Lim n!1 n2 n2 1 = 1 Therefore, the term inside the arctangent is going to 1, so lim n!1 arctan n2 n2 1 = arctan(1) = ˇ 4 12Does the series X1 n=2 1 n2 p n converge or diverge?



Lim N 1 N 2 Sec 21 N2 2 N 2 Sec 24 N 2 1 Nsec 21 Equals Sarthaks Econnect Largest Online Education Community
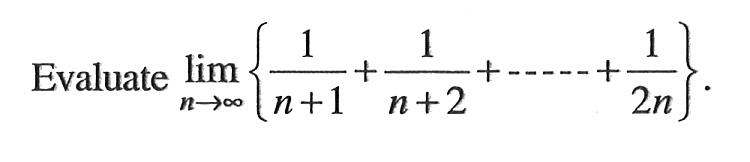



Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection
Thank you in advanceShort Solution Steps \ { \frac { ( n 1 ) ( n 2 ) } { 2 n ^ { 2 } } \} { 2 n 2 ( n 1) ( n 2) } Use the distributive property to multiply n1 by n2 and combine like terms Use the distributive property to multiply n 1 by n 2 and combine like terms \frac {n^ {2}3n2} {2n^ {2}} 2 n 2 n 2 3 n 2`Lim_(n>oo)1/n^2 * sec^2 (1/n^2)2/n^2 * sec^2 (4/n^2)1/n * sec^2 1` JEE Main 21 4th session starts from Aug 26, application last date extended
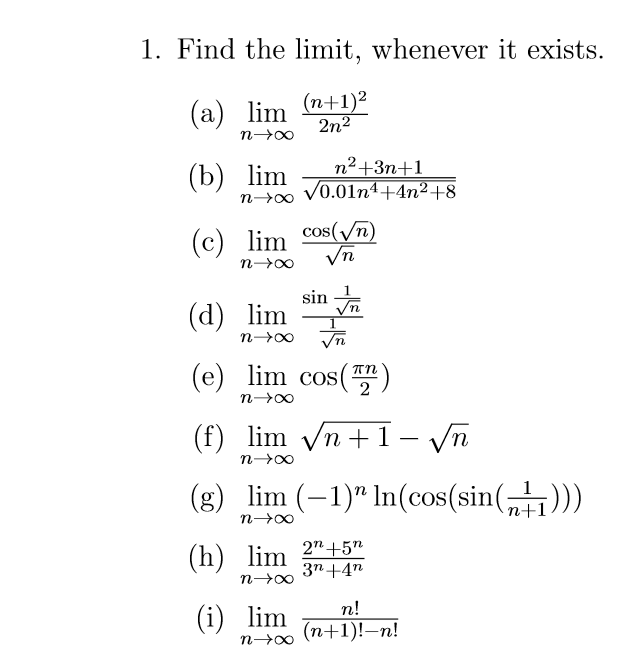



Find The Limit Whenever It Exists A Lim N Chegg Com




Sol 2 Functions And Mappings Complex Analysis
Value of lim n → ∞ (1 n 3 n 2 n 2 c o s n Elaborating n ln (1 n 3 n 2 n 2 c o s n ) = n ln (1 n 1 / n 2 c o s (n) / n 2Lim (1n22n23n2nn2) bằng A B 0 C 13 D 12Lim n ∞ ( 1 n 1 1 n 2 1 n 3 ⋯ 1 n 2 n ) Show transcribed image text Expert Answer Who are the experts?




Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection
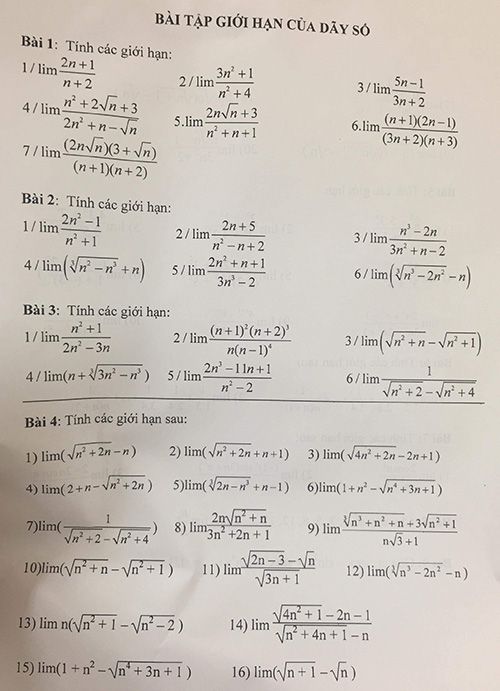



Tinh Giới Hạn Lim 2n 1 N 2 Lim 3n 2 1 N 2 4 Toan Học Lớp 11 Bai Tập Toan Học Lớp 11 Giải Bai Tập Toan
2n6 = 2 (n3), so goodbye n3 term, and it should go that way all the way downIn general, math\displaystyle\lim_{n\to\infty}\left(1\frac{x}{n}\right)^n=e^x/math Plugging in mathx=2/math math\displaystyle\lim_{n\to\infty}\left(1JEE Main 21 admit card for session 3 released Check important details related to the JEE Main 21 exam such as exam timing, venue, time slot etc




The Limit Does Not Exist Or Does It Ppt Download



Link Springer Com Content Pdf 10 1007 2f978 3 7091 6146 3 12 Pdf
\left( n 1 \right)!} \right\ \ = \lim_{n \to \infty Is the sequence {n/(n^21)} convergent, and if so, what is it's limit? Homework Statement find lim(n\\rightarrow\\infty (1/n^2 2/n^2 3/n^2 n1/n^2 ) Homework Equations b3 The Attempt at a Solution /b I could guess that the limit is zero but i dont know howto prove it



Www Jstor Org Stable




Show That Lim N Tends To Infinity 1 N 1 N 1 1 N 2 1 3n Log 3 Brainly In
See Answer Check out a sample Q&A here Want to see this answer and more?1 lim 1n 2n 1 1 1 = ? Evaluate lim(n→∞) {(n^6 6n^5 12n^4 1)^1/3 – (n^4 4n^2 6n 1)^1/2} asked in Limit, continuity and differentiability by Raghab ( 504k points) limits




Prove The Following Using The Definition Of A Limit Chegg Com



Www Math Univ Toulouse Fr Monnier Ct 19corrige Pdf
3n nn fullscreen check_circle Expert Answer Want to see the stepbystep answer?The value of n → ∞ lim 2 n sin 2 n a for a = 0 is equal to View solution The value of the n → ∞ lim n 2 1 n 2 − 1 1 n 2 − n 2 1 n 2 − ( n − 1 ) 2 1 isAs, math2^n > 0/math for all mathn \in \mathbb{N}/math and mathn!



Http Www D Umn Edu Jgreene Honors calculus Exam 3 11 Sol Pdf




Ex 7 8 4 Integrate X2 X Dx By Limit As A Sum Ex 7 8
If the sum of the first ten terms of the series ( 1 3 5) 2 ( 2 2 5) 2 ( 3 1 5) 2 4 2 ( 4 4 5) 2 , is 16 5 m, then m is equal to 7 Let p = lim x → 0 ( 1 tan 2 8 For x ϵ R, f ( x) = log 9 For x ∈ R, x ≠ 0, x ≠ 1, let f 0 ( x) = 1 1 − x and f n 1 ( x) = f 0 ( f n ( x)), n = 0, 1, 2,Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled> 0/math for all mathn \in \mathbb{N}/math So, math\dfrac{2^n}{n!} > 0/math for




N Ool An 2 2n 2 Limm 2n 1 2n Lim 00 2n 1 2 2n Nag 2n 1 2n N 00 N 1n Lim The Ratio Test Exercises Test Meme On Me Me




Telescoping Series Wikipedia
\\lim_{n \to \infty} \left \frac{\left( n 2 \right)!Tìm lim (1/căn (n^21) 1/căn (n^22) 1/căn (n^2n) Hoc24 Toán Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Bài 1 Giới hạn của dãy số Bài 2 Giới hạn của hàm số Bài 3 Hàm số liên tục Bài lim(n→∞)(n/n2 12 n/n2 22 n/n2 32 1/5n) is equal to (1) tan1(2) (2) π/2 (3) tan1(3) (4) π/4 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries




Mth3101 Advanced Calculus Chapter 2



Grenzwert Von Lim 1 N 1 N 2 N Mathelounge
x = λ n we have lim n→∞ n2(a1 n a− 1 n − 2) = lim x→0 2λ2( cosh(x) −1 x2) but cosh(x) = 1 x2 2!Now let us multiply and divide by the heighest power n^2 ==> lim (1 1/n)/ 2 (1 3/n 1/n^2) when n > inf ==> lim = (10)/2 (10 0) = 1/2 Then the limit = 1/2 Approved by eNotes Editorial 1 Determine whether the sequence converges or diverges If it converges, find its limit {itex\frac{n}{2 n}/itex} ∞ n = 1 I know that we have to use L'Hopital's rule for this, because as n increases, both the numerator and the denomator approach infinity




N Ool An 2 2n 2 Limm 2n 1 2n Lim 00 2n 1 2 2n Nag 2n 1 2n N 00 N 1n Lim The Ratio Test Exercises Test Meme On Awwmemes Com




ลำด บและอน กรม
Explain your answer Answer For large n, the n2 should dominate the p n, so let's do a limit comparison to the convergent series P 1 n2 lim n!1 1 n2 p n 1 n2\left \begin{array} { l } { \lim \frac { 2 n ^ { 2 } n 3 } { 3 n ^ { 2 } 2 n 1 } } \\ { \lim \frac { n ^ { 4 } } { ( n 1 ) ( 2 n ) ( n ^ { 2 } 1IIT JEE 12 Determinants 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is KCET 6 The locus represented by x y y z = 0 is KCET 18 Three Dimensional Geometry 7 If f (x) = sin − 1 ( 2 x 1 x 2), then f' ( 3) is




If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange




Answered S 1 Is N N 1 Convergent Divergent Check Bartleby
L'Hospital's Rule states that the limit of a quotient of functions is equal to the limit of the quotient of their derivatives lim n → ∞ n 2 n = lim n → ∞ d d n n d d n 2 n lim n → ∞ n 2 n = lim n → ∞ d d n n d d n 2 n Find the derivative of the numerator and denominator Tap for more stepsExperts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!*Click here👆to get an answer to your question ️ n→∞1/n∑ r = 1^2nr/√(n^2r^2) equals Join / Login > 11th > Applied Mathematics > Limits and Continuity > Methods of evaluating limit of a function > n→∞1/n∑ r = 1^2nr/√(n^2r^2 maths n → ∞ lim n 1 r = 1 ∑ 2 n n 2 r 2
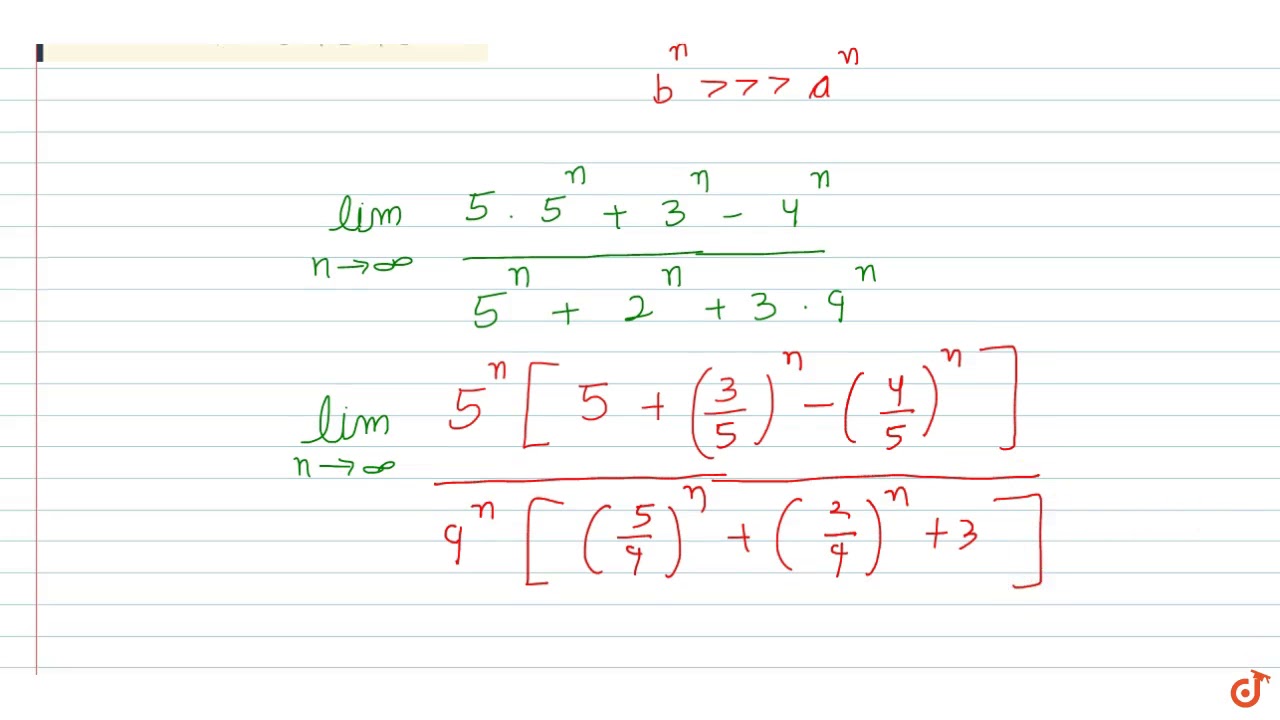



Lim N Gtoo 5 N 1 3 N 2 2n 5 N 2 N 3 2n 3 Youtube




6 1 3 Areas As Limits Of Riemann Sums
IIT JEE 12 Determinants 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is KCET 6 The locus represented by x y y z = 0 is KCET 18 Three Dimensional Geometry 7 If f (x) = sin − 1 ( 2 x 1 x 2), then f' ( 3) is lim(n →∞){1/n2 2/n2 3/n2 n/n2} is (A) 1/2 (B) 0 1 (D) ∞ If x is a real number in 0, 1, then the value of lim(m →∞) lim(n →∞) 1 cosIn this video, we are going to evaluate our limit, so, in order to evaluate we are going to use the definite integral for the evaluation of this limits and y




Bai 5 Tim Cac Giới Hạn Sau 1 3 5 2n 1 1 Lim Ds1 3 4 Lim Ds1 N N 1 1 2 2 3 3n 4 Ds1 2 1 2 3 N 2 Lim N2 3 12 22 3 N 3 Lim 1 1 1 5



Link Springer Com Content Pdf 10 1007 2f978 3 7091 6146 3 12 Pdf
N→∞lim r=1∑n n2 r2r = n→∞lim r=1∑n n1 1(nr )2(nr ) = ∫ 01 1x2x dx= 21 ∫ 01 1x2d(x2) = 21 log(1x2)∣01 = 21 log(2) so we have lim n→∞ n ∏ k=1(1 k n2) ≤ lim n→∞ (1 n 1 2n2)n = √e Considering now the limit lim n→∞ n ∏ k=1(1 k − 1 n2) instead, we conclude lim n→∞ n ∏ k=1(1 k n2) = √e Answer linkHow can we compute the following limit $$\lim_{n\to\infty}(11/n^2)(12/n^2)\cdots(1n/n^2)$$ Mathematica gives the answer $\sqrt{e}$ However, I do not know to do it




Tcme Suites




3 Find 7t 1 Lim N Sin 3 Lim Arcsin G N 00 N 100 Cos N Homeworklib
Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Transcribed image text Previous question Next question⋯ then lim n→∞ n2(a1 n a− 1 n − 2) = λ2 but λ = logea then lim n→∞ n2(a1 n a− 1 n − 2) = (logea)2 Answer linkIn this video, we are going to evaluate a nice limit which may be importantTo evaluate this limit, I used "sum of series with the help of definite integral




Log B Log A Log Bla N 1 N 2 N




Chapter 1
Lim(√n 10−√n) lim ( n 10 − n) có giá trị là bao nhiêu?



Www Mtholyoke Edu Courses Jmorrow Calculus Ii Factexsolns Pdf




Oneclass Let An Sqrt N 2 1 2n 1 A Find Lim An N Tends To Infinity B Does Sigma An Between N




Answered 2i Part A Lim Ei N 2 N V N I 1 N 00 Bartleby




Lim N Oo 1 N 2 N 1 3 N 2 N 1 1 2 2 2 3 2 N 2



Search Q Limit N Tends To Infinity 1 N Tbm Isch




How To Prove Lim N To Infty Frac 1 Gamma N 2 1 Int 0 N T N 2 E T Dt 1 Newbedev
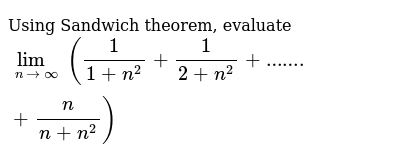



Using Sandwich Theorem Evaluate Lim N Oo 1 1 N 2 1 2 N 2
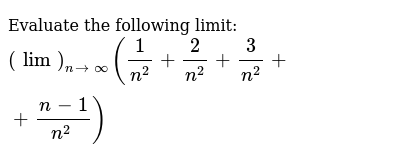



Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N




Evaluate Lim N 1 N 1 N 1 1 N 2 1 3n Youtube




Video 2533 Limit Of Sequence 1 1 N 2 N Practice Youtube




Example 25 Find Integral X2 1 Dx As Limit Of A Sum Examples




Math 121 Homework 7 Solutions




Ism Et Chapter 8
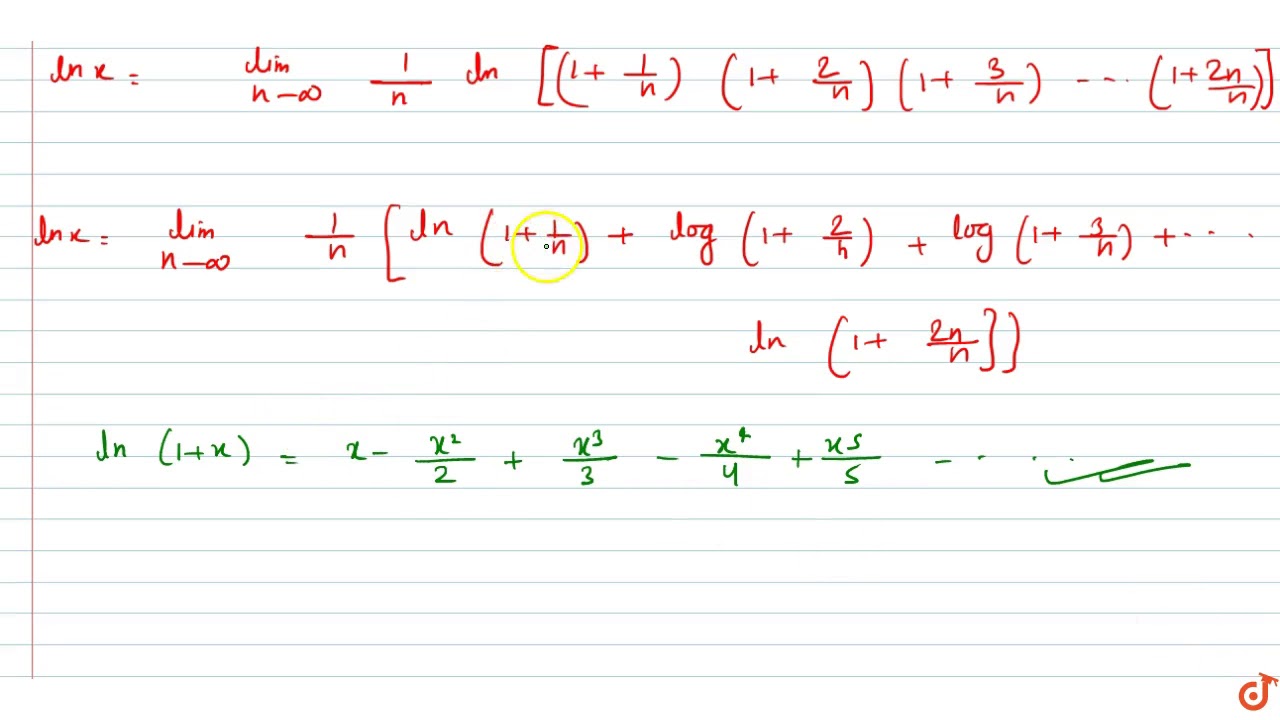



Lim N Gtoo N 1 N 2 3n N 2n 1 N Is Equal To Youtube



Www3 Nd Edu Dgalvin1 S08 Exam3 Solns Pdf




Faq Fr Sci Maths Les Utilisateurs De Fr Sci Maths Version Pdf Free Download



1




Calameo Ex 112 113 P 60




Calculus Find The Radius Of Convergence For 3n Prezentaciya Onlajn




Limn 4n2 N 2n 1 4



Search Q 1 Infinity Tbm Isch




Lim N 2 N 1 N 2 N 1 N N 1 N Is Infinity Askiitians




Also Known As Hysterical Calculus Prezentaciya Onlajn




Take For Granted That The Limit Lim 1 1 N N Chegg Com




Convergence Of The Series Sum Limits N 1 Infty Frac Left 1 Frac1n Right N 2 3n 2 2 E N Mathematics Stack Exchange




Ma2108s Tutorial 5 Solution




Lim N Tends To Infinity 1 2 2 2 N 2 N 4 Brainly In




In Showing Integer Sum 1 2 3 N By L Hopital Rule Why They Take Lim As R Approaches To 1 In One Of Steps Why 1 Mathematics Stack Exchange



Limit Of Sequence Lim N 1 Cos 2 N Physics Forums



Www3 Nd Edu Dgalvin1 S08 Exam3 Practice Solns Pdf
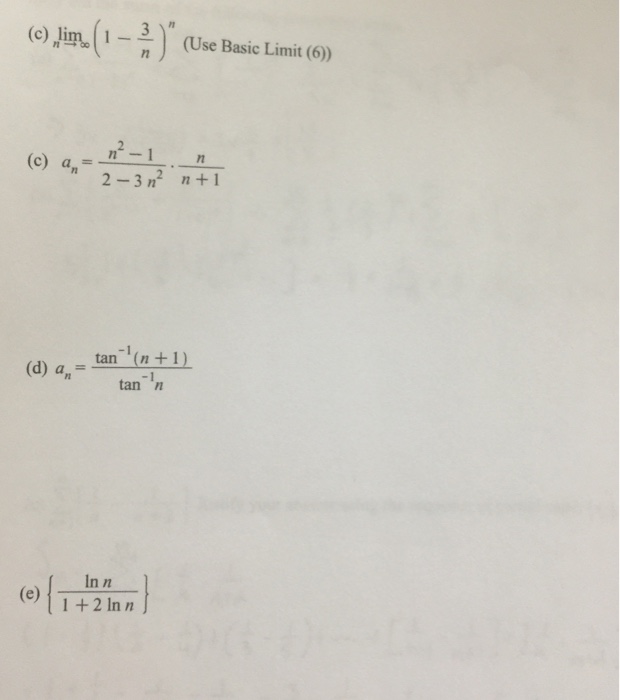



Lim N Rightarrow Infinity 1 3 N N Use Basic Limit Chegg Com
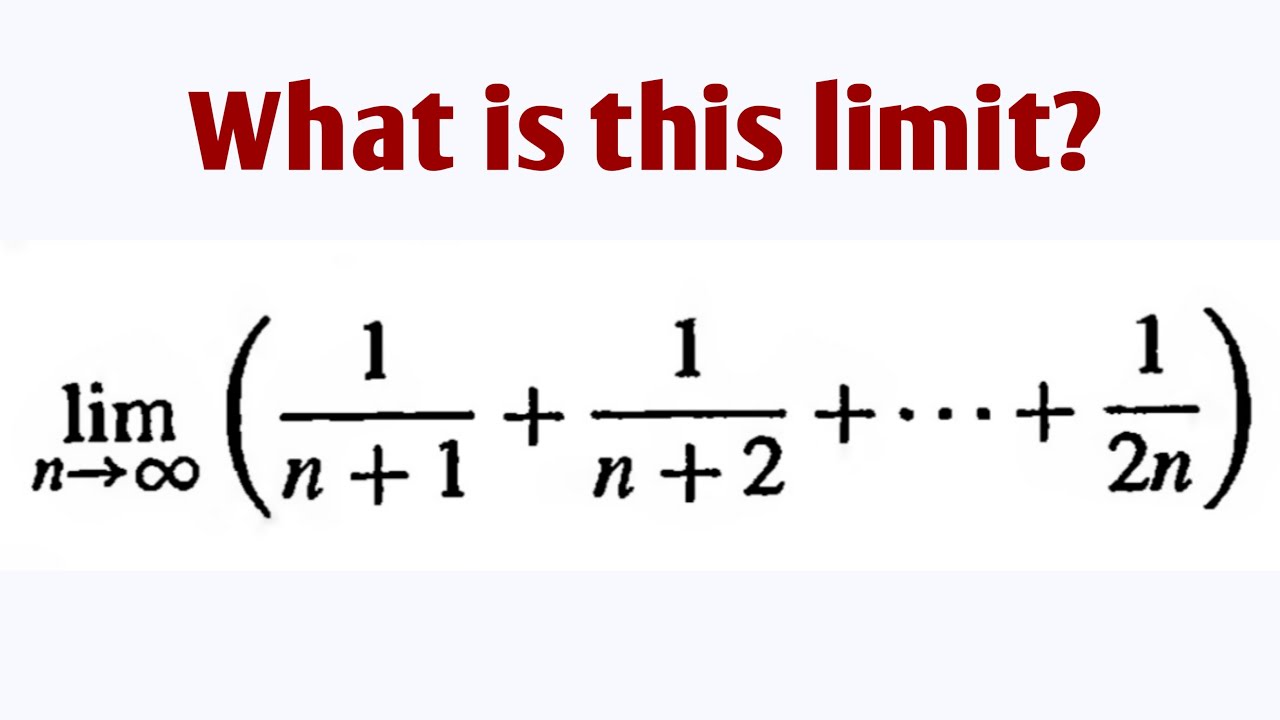



Lim 1 N 1 1 N 2 1 2n What Is This Limit Youtube




Stolz Cesaro Theorem Online Presentation




Find The Limit Of 1 N 1 1 N 2 1 N 3 1 6n As N Tends To Infinity Youtube



Www Askiitians Com Forums Integral Calculus Summation R 1 To N Tr N N 1 N 2 N 3 8 Find L Htm




For The Limit As N Approaches Infinity For Sum Of Chegg Com




Ex 7 8 1 Integrate X Dx From A To B By Limit As A Sum




Solve N 1 1 N 2 2 1 N 2 N 1 N 2 Is Equal To



Http Www Webassign Net Resources Rogacalcet2 Testing Series Et Pdf




Find The Limit Of 1 N 1 1 N 2 1 N 3 1 6n As N Tends To Infinity Youtube




Limit Replace 1 By 0 Mathematics Stack Exchange



1




Calameo Page 52




Science Infinite Series Module Units Unit 1 1 1 Infinite Sequences 1 1 06 Limit Laws Example Ubc Wiki




Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N




N 2 Frac 2 N 2 Lim N Rightarrow Infty Left Left 1 Frac 1 N 2 Right Frac 2 2 Left 1 Frac 2 2 N 2 Right Frac 1 N 2 Dots Left 1




Pdf Finding Exact Values For Infinite Sums




Proof Of Lim N To Infty Sqrt N N 1 Mathematics Stack Exchange




1 2 1 4 1 8 1 16 Wikipedia




ลำด บและอน กรม




Math 101 Homework 2 Solutions 1 Evaluate The Limits N



Limit Limit N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community




Chapter 3 Cbu




6 1 3 Areas As Limits Of Riemann Sums



Lim N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community
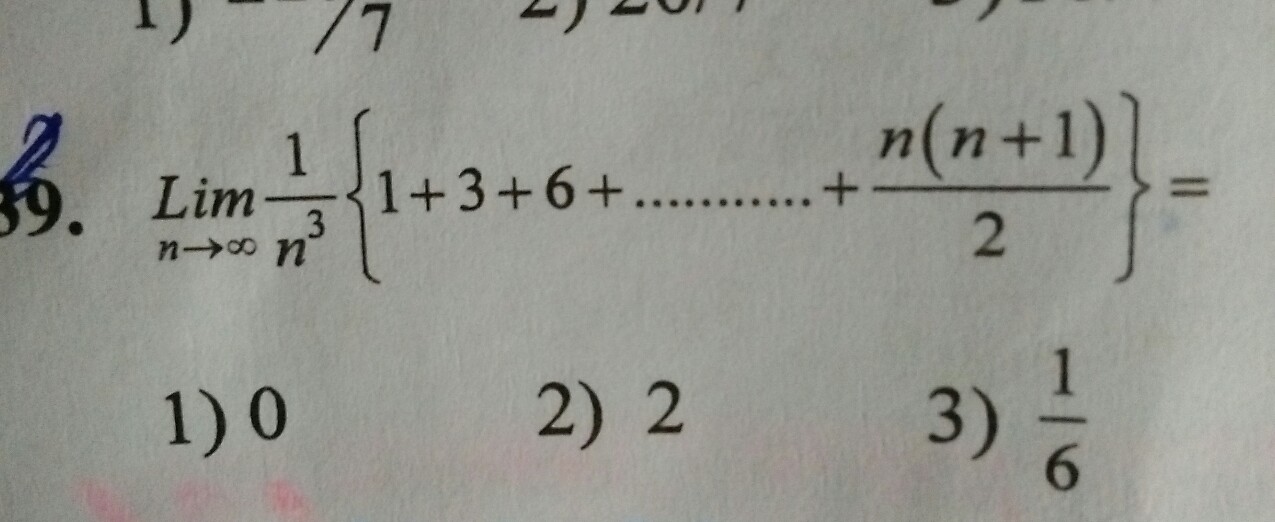



Lim N Infinity 1 N 3 1 3 6 N N 1 2



What Is The Limit Of 2 N 1 3 N 1 2 N 3 N As N Tends To Infinity Quora



What Is Lim 3 N 2 N 1 2n When N Tends To Infinity Quora



How To Evaluate The Limit Of Math Lim N To Infty Dfrac 1 N 1 Dfrac 1 N 2 Dots Dfrac 1 2n Math Quora



Comment Calculer La Limite Math Lim Limits N To Infty Sum Limits K 1 N Frac 1 Sqrt N 2 2k Math Quora



2




Giới Hạn Day Số 2n 4n 3n 3 3 Lim 2n2 N 2 4 Lim 1 N 2n 2 Lim 6n 2n 1 I Lim 5n N 3n 5 N 5n 7 N 2n 7n 3n 2




Determine Whether The Series Sum N 1 Infty 1 N 1 Frac 1 N N 2 Converges Absolutely Or Converges Conditionally Or Diverges Mathematics Stack Exchange
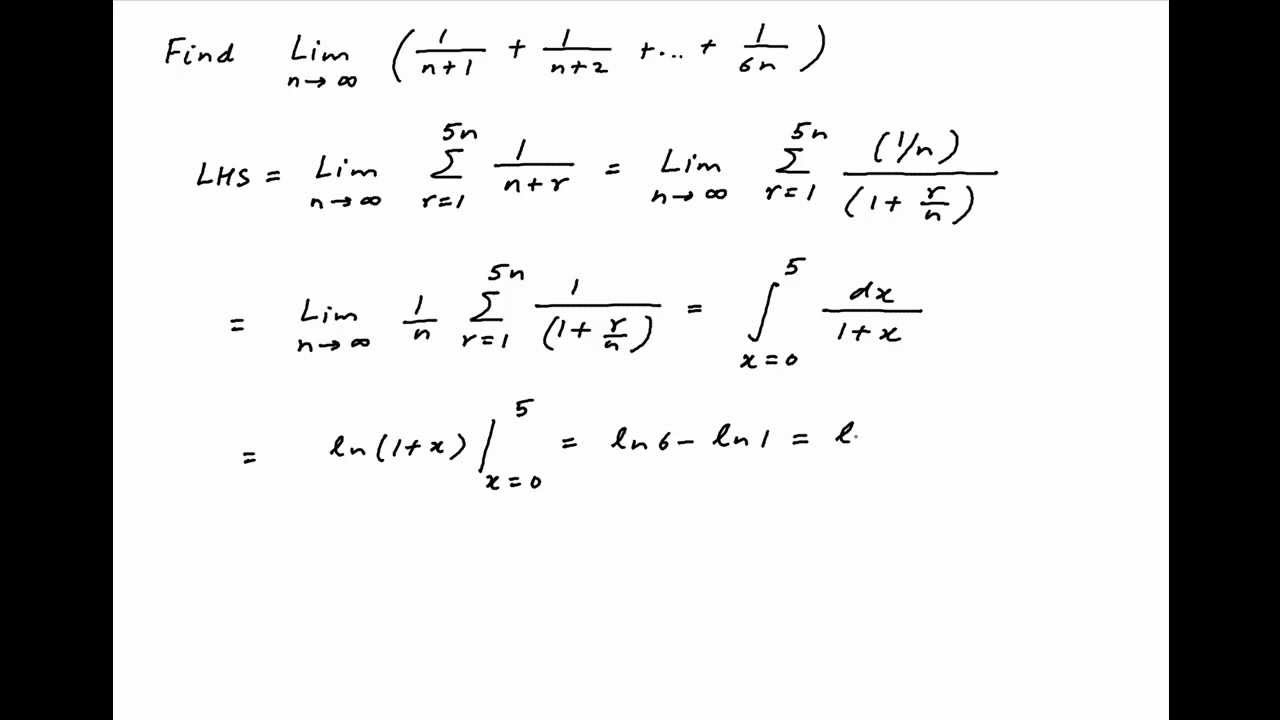



Find The Limit Of 1 N 1 1 N 2 1 N 3 1 6n As N Tends To Infinity Youtube



2




Wallis Product Wikipedia Republished Wiki 2




Exercise 02 Studocu




ลำด บและอน กรม
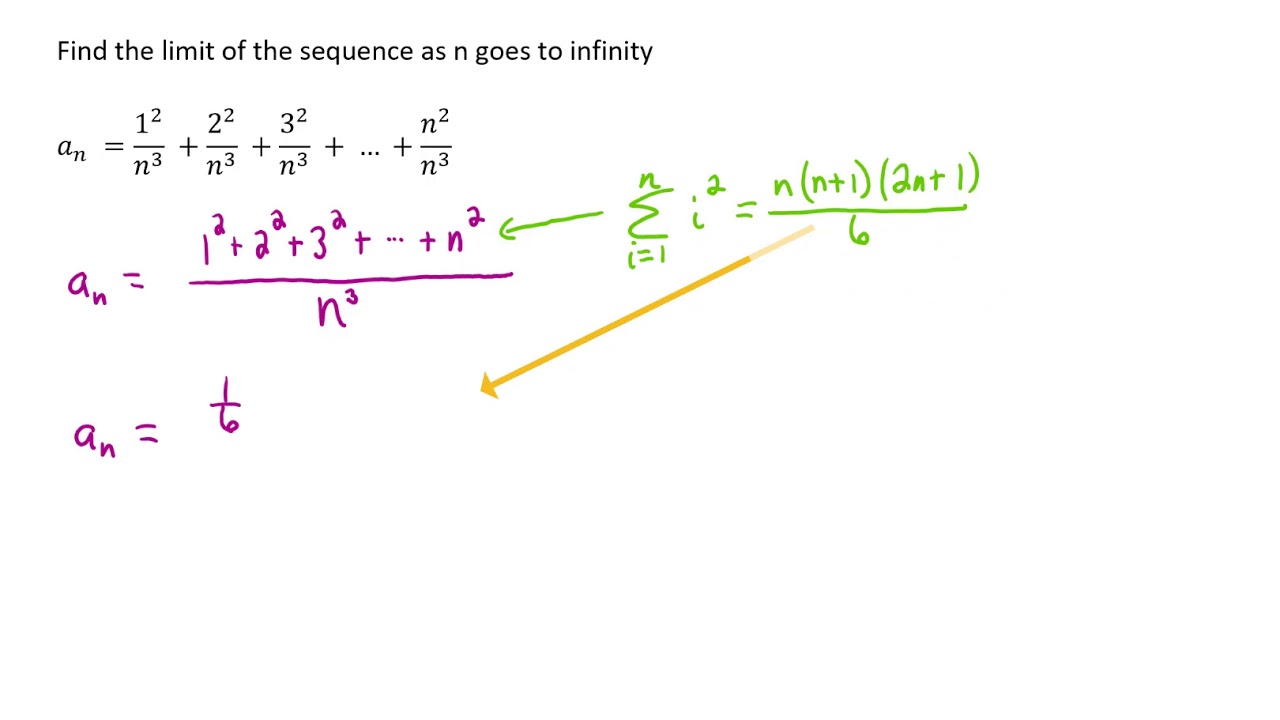



Find The Limit Of 1 N 3 2 2 N 3 3 2 N 3 N 2 N 3 As N Goes To Infinity Sequences 2 Youtube




Lim N Oo 1 2 2 2 3 2 N 2 N 3 Is Equal To A 1 B C 1




A Limit Involving Binomial Coefficients Lim N To Infty 1 N Sum K 1 N 1 K N Choose K 1 K Frac12 Mathoverflow




How To Evaluate Lim N Tends To Infinty 2 N 1 2 N 1 Without The Hospital Rule Quora




Suite Exercice
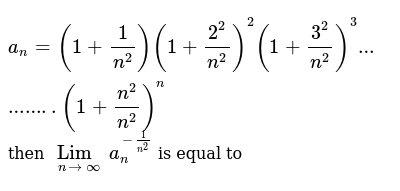



A N 1 1 N 2 1 2 2 N 2 2 1 3 2 N 2 3 1



0 件のコメント:
コメントを投稿